| Цуьнах лаьцнаPythagorean tiling based on 5 and 12.svg |
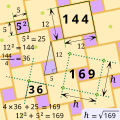
English: A right triangle has perpendicular edges of lengths  Denoted  its hypotenuse its hypotenuse length is the dimension of a square minimal pattern of the “ Pythagorean tiling” of the image, by squares of dimensions  In such a tiling, any square tile of one of the two dimensions adjoins, by any edge, exactly one square tile of the other dimension. Study these tilings enables us to prove the Pythagorean theorem, valid for any right triangle. In this particular proof  four congruent quarters of a great square tile surround a small square tile, and the five polygons together form a repetitive square pattern of the periodic tiling. Therefore, this square pattern has an area  and its dimension is  This square root equals a natural number, see “ Pythagorean triple”.
Français : Un triangle rectangle a des côtés perpendiculaires de longueurs  Désignée  la longueur de son hypoténuse est la dimension d’un motif minimal carré du “pavage de Pythagore” de l’image, par des carrés de dimensions  Dans un tel pavage, n’importe quel élément carré d’une des deux dimensions jouxte, par n’importe quel côté, un élément carré et un seul de l’autre dimension. Étudier ces pavages nous permet de prouver le théorème de Pythagore, qui s’applique à n’importe quel triangle rectangle. Dans cette preuve particulière  quatre quarts superposables d’un grand élément carré entourent un petit élément carré, et les cinq polygones forment ensemble un motif carré répétitif du pavage périodique. Par conséquent, ce motif carré a une aire égale  Et sa dimension est  Cette racine carrée est un nombre entier naturel, voir Triplet pythagoricien. |