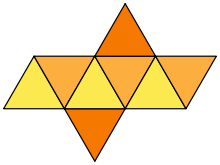
БархӀсонарниг

Окта́эдр (желт. οκτάεδρον схьадаьлла οκτώ «бархӀ» + έδρα «бух») — бархӀ са болу сенашдерг.

Нийса октаэдр
(хьийза модель)
Тайпа	нийса сенашдерг
Комбинаторика
Дакъалгаш
Баххьийн конфигураци	4.4.4
Шалха сенашдерг	къуб
Баххьийн куц
Баржам
Классификаци
Билгалонаш	O aT
Шлефлин сийлалла	$\{3,4\}$ $r\{3,3\}$ йа ${\begin{Bmatrix}3\\3\end{Bmatrix}}$
Витхоффан сийлалла	4 | 2 3
Дынкинан диаграмма
Хьийзаран тоба	$O$
Бараман хаамаш
Ши са болу маьӀиг	$\arccos \left(-{\frac {1}{3}}\right)\approx 109.5^{\circ }$
Боьххьера дегӀан маьӀиг	$2\pi -8\arcsin \left({\frac {1}{\sqrt {3}}}\right)$ $\approx 1.35935$ ср
Викиларми чохь медиафайлаш

Октаэдран гуонахьара кхачо

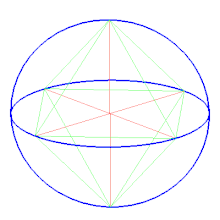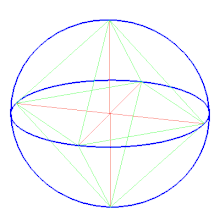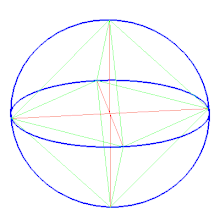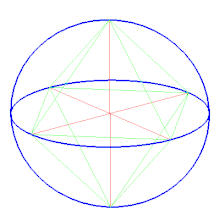
Ни́йса окта́эдр аратаьӀна нийса сенашболчарех пхеаннах цхьаъ йу, царех олу Платонан догӀмаш; цуьнан маьӀигаш — бархӀ агонаштера кхосаберг. Нийса октаэдр:

• къубан шалха;
• тетраэдран йуьззина хадор;
• муьлхха а кхаа ортогоналан агӀонийн йеакӀовн бипирамида;
• гӀалин куьпийн метрикера кхаабарамера горгал.

Октаэдр — гипероктаэдр гӀоле кхета йукхара кхетаман кхаабарамера вариант.

Нийса октаэдр

Нийса октаэдран 8 кхо са болу маьӀиг йу, 12 пӀенда а, 6 бохь а бу, хӀора цуьнан боьххьехь цхьаьнакхета 4 пӀенда.

Барамаш

Нагахь пӀендин бохалла а санна балахь, тӀаккха октаэдран гонахьара кхачонан радиус хуьлу

$r_{u}={\frac {a}{2}}{\sqrt {2}}\approx 0.7071067\cdot a$,

Октаэдран йукъайиллина кхачонан радиус лара таро йу формулица:

$r_{i}={\frac {a}{6}}{\sqrt {6}}\approx 0.4082482\cdot a.$

Шина маьӀиган са: ${\textstyle \alpha =2\varphi \approx 109,47^{\circ }}$, кхузахь ${\textstyle \varphi =\arccos \left({\frac {\sqrt {3}}{3}}\right)}$.

Дерриг пӀендарчех хьакхалуш йолу ахйукъайиллина кхачонан радиус хуьлу

$r_{m}={\frac {a}{2}}=0.5\cdot a$

Ортогоналан проекцеш

Октаэдран хуьлу йиъ башха пӀендо боххьо, сено маьӀигца центраци йина ортогоналан проекци. ШолгӀа а, кхоалгӀа а меттиг хуьлу Коксетеран экъа B₂ а, A₂ а санна.

Ортогоналан проекцеш

Центраци йина	ПӀенданца	Нормалца маьӀиган	Бохьца	МаьӀигца
Васт
Проекцин симметри	[2]	[2]	[4]	[6]

Кхачонан мозаика

Октаэдр доьхьала таса тарло кхачонан мозаика санна, проекци экъана тӀейаккха тарло стереографин проекцин гӀоьнца. И проекци конформан йу, Ӏалашбо сенаш, амма ца йо йохалла а, майда а. Кхачонан тӀера кийсакаш гойту экъанан тӀехь гонан Ӏад санна.

	Кхосаболчун- йукъйаккхар
Ортогоналан проекци	Стереографин проекци

Декартан координаташ

ПӀенда бохалла ${\textstyle {\sqrt {2}}}$ болу октаэдр хӀотто тарло координатийн йуьххье, цуьнан баххьаш координатийн семнаш тӀехь лаьтташ. Баххьийн декартан координаташ тӀаккха хир бу

(±1, 0, 0);

(0, ±1, 0);

(0, 0, ±1).

x-y-z санийса координатийн системера йукъ тӀадамехь (a, b, c) а, радиус r йолу октаэдр — иза (x, y, z) дерриг тӀадамийн дукхалла йу

$\left|x-a\right|+\left|y-b\right|+\left|z-c\right|=r.$

Площадь и объём

ПӀендин a йохалла йолу нийса октаэдран тӀехулара майда хуьлу

$S=2a^{2}{\sqrt {3}}\approx 3.46410162a^{2}$

Кхосаболчун антипризма

Цхьаьнатайпана антипризмийн доьзал n.3.3.3

Сенашдерг
Мозаика
Конфигураци	V2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...∞.3.3.3

ЙеакӀовн бипирамида

Бипирамидийн доьзал

Сенашдерг
Мозаика
Конфигураци	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...V∞.4.4

Хьажа кхин а

• Октаэдран граф
• Седакепара октаэдр
• Координацин теори
• Октаэдран симметри
• Октаэдран терахь
• Хадийнаромбан додекаэдр
• Триакисоктаэдр
• Хадийна октаэдр
• Йукъйаьккхина октаэдран терахь

Литература

• Большая советская энциклопедия
• Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158, вып. 8. — DOI:10.1016/j.dam.2009.08.002.
• Douglas J. Klein. Resistance-Distance Sum Rules // Croatica Chemica Acta. — 2002. — Т. 75, вып. 2. Архивйина 2007  шеран  22 июнехь.
• R. Williams. Chapter 5 The Kaleidoscope, Section: 5.7 Wythoff's // The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979.

Хьажоргаш

• Weisstein, Eric W. Octahedron(ингалс.) на сайте Wolfram MathWorld.
• Klitzing Polytopes, 3D convex uniform polyhedra
• Editable printable net of an octahedron with interactive 3D view
• Paper model of the octahedron
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • Conway Notation for Polyhedra Try: dP4